Time Complexity (시간 복잡도)

* 이 글은 제로초님의 강의 '비전공자의 전공자 따라잡기 - 자료구조(with JavaScript)' 를 듣고 정리하였습니다.

출처 : https://www.zerocho.com/category/Algorithm/post/57ea2987fdea850015313534

 

 

목차

시간복잡도란?

알고리즘을 수행하는 데 평균적으로, 또는 최악의 경우 얼마 만큼의 시간이 걸리는 지 보여주는 것.
(💡 공간복잡도란? 알고리즘이 얼마만큼의 메모리를 잡아먹는 지 보여주는 것)

 

그렇다면 알고리즘의 로직을 코드로 구현할때, 시간복잡도를 고려한다는 것은 무슨 의미일까?

 

알고리즘의 로직을 코드로 구현할때, 시간복잡도를 고려한다는 것은 

"입력값의 변화에 따라 연산을 실행할때 연산 횟수에 비해 시간이 얼마만큼 걸리는가?" 라는 말이다.

 

즉, 효율적인 알고리즘을 구현한다는 것은 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 말이다.

📍표기법(시간 복잡도를 표시하는 방법)

알고리즘의 성능을 수학적으로 표현해준다.
표기법이 필요한 이유는 자료구조, 알고리즘의 성능을 표기하기 위해서 사용된다.

• Big-O(빅오) 표기법 : 최악의 경우
• Theta(세타) 표기법 : 빅오===빅오메가 동등한 경우(공통부분), 최선과 최악의 중간이 평균적인 복잡도
• Big-Omega(빅오메가) 표기법 : 최선의 경우

📍빅오 표기법(Big-O)

최악의 경우에서 최선의 효율을 찾아야 하기 때문에 대부분 시간 복잡도는 빅오표기법을 사용한다.
알고리즘의 실제 수행시간을 표기한다기 보단 데이터나 사용자의 증가율에 따른 알고리즘 성능을 예측하는게 목표이므로 상수의 경우 모두 1로 취급한다.

 

표로 더 쉽게 알아보자면...!

 

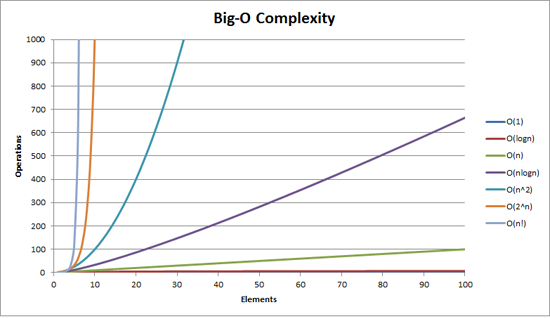
기울기가 가파를 수록 성능이 안좋은 것! (n!는 하늘을 뚫고 있다...!)

 

n은 배열의 길이, 데이터의 총 개수를 n이라고 표시한다면,

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) ... < O(2^n) < O(n!)

😁good —————————————————————————😭bad

• n의 앞의 수를 개수라고 한다.
• n의 뒤의 수를 지수라고 한다.(지수는 반복문의 중첩횟수에 밀접한 관계가 있다.)
• n뒤에 붙는 수가 작을 수록 더 빠르다.
• 시간이 적게 걸릴 수록 성능이 좋다.

예를 들어 n이 100개일 경우 n하나당 처리 속도가 0.01초가 걸린다고 생각해보면,

O(nlogn)은 4.6초, O(n^2)는 100초가 걸린다. 그렇다면 O(2^n)은?? 최악🤮

📍코드로 쉽게 생각해보기!

👉O(logn) : for문의 i가 곱하기, 나누기, 배수 등 절반이 되는 상황일때(i*n)

function O_log_n_algorithm(n) {
  for (let i = 0; i < n; i*=2) {
    // ...
  }
}

• 예를 들어 1부터 100까지 숫자 중에서 원하는 숫자 하나를 찾는 UPDOWN 게임을 한다면 1부터 100까지 다 불러서 찾는 방법은 O(n), 50을 부르고 해당 숫자의 또 반 절씩 잘라 나가면서 찾은 방법은 O(logn)

👉O(n) : for문(i++)

function O_n_algorithm(n) {
  for (let i = 0; i < n; i++) {
    // ...
  }
}

👉O(nlogn) : 이중 for문일때 for문(i++) 과 for문(j*n) 이런 상황 일 경우

function O_n_log_n_algorithm(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j*=2) {
      // ...
    }
  }
}

👉O(n^2) : 이중 for문(i++)

function O_n_2_algorithm(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      // ...
    }
  }
}

👉O(n^3) : 삼중 for문(i++)

function O_n_3_algorithm(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      for (let k = 0; k < n; k++) {
        //...
      }
    }
  }
}

 

📍마무리

시간 복잡도가 무엇인지 정확히 알게되었고, Big O 표기법을 사용하여 성능을 결정하는 방법을 배웠다.